研究の掃溜ノオト
since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。
メビウス函数
このメビウス函数μ(n)は
・n=1のとき μ(n)=1
・n が平方数で割り切れる時 μ(n)=0
・n がk個の素数で因数分解されるとき μ(n) = (-1)^k
というなんともけったいな函数ですが整数論では大変重要だそうです。
ちなみに僕は整数論ほとんどやったことないです(*´Д`)
定義域が正整数である函数は数論的函数というそうです
定義域が複素数だと複素関数というのとおんなじような感じですね
メビウス函数はもちろん数論的函数です
二つの数論的函数 f(n), g(n) の間に次のような積を定義します
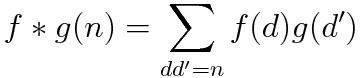
n d d'は自然数です. この積はディリクレ積と呼ばれます. f*g(n) も数論的函数です.
ディリクレ積の単位元は次のような数論的函数e(n)です.
・n = 1 の時 e(n) = 1
・n > 1 の時 e(n) = 0
これが単位元になることはディリクレ積の定義から明らかでしょう
恒等的に1であるような数論的函数η(n)を考えましょう
すなわちη(0)=1, η(1)=1, η(2)=1, η(3)=1, ...
この数論的函数の逆元は何でしょうか?
逆元は逆元の定義より
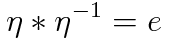
を満たすので逆元の値は以下の様に順番に計算していくことができます.
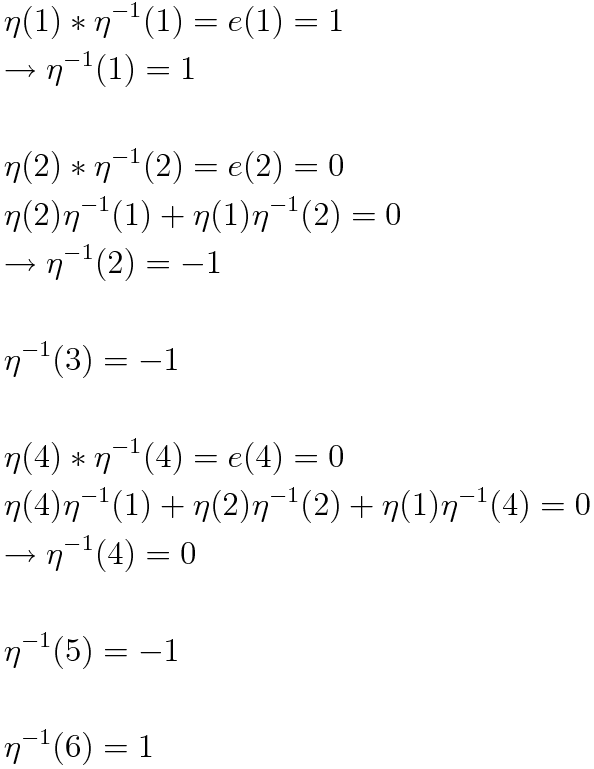
こんな数論的函数を見たことありませんか?
実はη の逆元はメビウス函数μ なのです.
このことからメビウスの反転公式
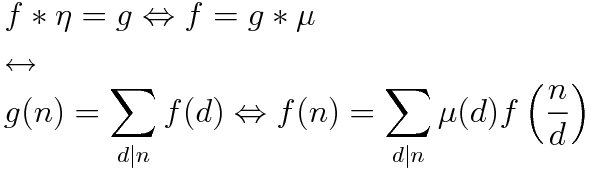
が簡単に導けます
・n=1のとき μ(n)=1
・n が平方数で割り切れる時 μ(n)=0
・n がk個の素数で因数分解されるとき μ(n) = (-1)^k
というなんともけったいな函数ですが整数論では大変重要だそうです。
ちなみに僕は整数論ほとんどやったことないです(*´Д`)
定義域が正整数である函数は数論的函数というそうです
定義域が複素数だと複素関数というのとおんなじような感じですね
メビウス函数はもちろん数論的函数です
二つの数論的函数 f(n), g(n) の間に次のような積を定義します
n d d'は自然数です. この積はディリクレ積と呼ばれます. f*g(n) も数論的函数です.
ディリクレ積の単位元は次のような数論的函数e(n)です.
・n = 1 の時 e(n) = 1
・n > 1 の時 e(n) = 0
これが単位元になることはディリクレ積の定義から明らかでしょう
恒等的に1であるような数論的函数η(n)を考えましょう
すなわちη(0)=1, η(1)=1, η(2)=1, η(3)=1, ...
この数論的函数の逆元は何でしょうか?
逆元は逆元の定義より
を満たすので逆元の値は以下の様に順番に計算していくことができます.
こんな数論的函数を見たことありませんか?
実はη の逆元はメビウス函数μ なのです.
このことからメビウスの反転公式
が簡単に導けます
PR
この記事へのトラックバック
トラックバックURL


この記事へのコメント
無題
無題