Gaussian Processes on Python

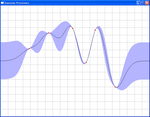
 Gaussian Processes のプログラムをPython+Pygame+Numpyの組み合わせで実装してみました。
クリックした点を通る関数をエラーバー付きで求めるというものです！



以下ソース

# -*- coding: cp932 -*-

import pygame

from pygame.locals import *

from numpy import *

from numpy.linalg import *

from math import *

 

SCR_W = 800 # 表示ウィンドウの横幅

SCR_H = 600 # 表示ウィンドウの縦幅

GRIDCOLOR = 180 # グリッドのグレースケール

 

def Kernel(x,y): # 共分散関数

    return exp(-((x-y)**2)/4000)

#    return cos(0.5*(x-y))*exp(-((x-y)**2)/4000)

 

def gp(data): #各ｘ軸での平均値と分散値の計算

    mean = []

    covariance = []

 

    if len(data[0]) < 1 : # 事前分布

        for x in range(800):

            mean.append(0)

            covariance.append(100.*Kernel(x,x))

        return mean,covariance

    

    num = len(data[0])

    kfunc = zeros((num))

    GRAM = zeros((num,num))

 

    for i in range(num): # 共分散行列の計算

        for j in range(num):

            GRAM[i][j] = Kernel(data[0][i],data[0][j])

    for i in range(num): # 観測ノイズの付加

        GRAM[i][i] += 0.005

 

    for x in range(800): # 各点の平均値と分散値の計算

        for i in range(num):

            kfunc[i] = Kernel(data[0][i],x)

        mean.append(float(matrix(kfunc) * matrix(GRAM).I * matrix(data[1]).T))

        covariance.append(float(100.*(Kernel(x,x) - matrix(kfunc) * matrix(GRAM).I * matrix(kfunc).T)))

    return mean,covariance

 

def main():

    data = [[],[]]

    mean , covariance = gp(data) # 事前分布代入

    origin = 300. * ones((800)) # 描画用原点の初期化

 

    pygame.init() # pygameの初期化

    screen = pygame.display.set_mode( (SCR_W, SCR_H) ) # 画面を作る

    pygame.display.set_caption('Gaussian Processes') # タイトル

 

    while 1:

        pygame.draw.rect(screen , (255, 255, 255), (0, 0, 800, 600)) # 画面消去

        for i in range(0,800,40): # グリッド描画

            for j in range(0,600,40):

                 pygame.draw.line(screen, (GRIDCOLOR,GRIDCOLOR,GRIDCOLOR), (0,j), (800,j))

                 pygame.draw.line(screen, (GRIDCOLOR,GRIDCOLOR,GRIDCOLOR), (i,0), (i,600))

 

        # 分散を多角形として描画

        cov1 = zip(range(800),list(origin - array(mean)-array(covariance)))

        cov2 = zip(range(800),list(origin - array(mean)+array(covariance)))

        cov2.reverse()

        pygame.draw.polygon(screen, (180,180,255), cov1+cov2, 0)

        # 事後平均値関数の描画

        pygame.draw.lines(screen, (0,0,0), False, zip(range(800),list(origin - array(mean))), 1)

        

        if len(data[0])>0 : # プロット点の描画

            for i in range(len(data[0])):

                pygame.draw.circle(screen, (255,0,0), (int(data[0][i]), int(300. - data[1][i])), 3)

 

        pygame.display.flip() # 画面を反映

 

        for event in pygame.event.get(): # イベントチェック

            if event.type == MOUSEBUTTONDOWN: # マウスボタン取得

                # プロット点の代入

                data[0].append(float(pygame.mouse.get_pos()[0]))

                data[1].append(float(300. - pygame.mouse.get_pos()[1]))

                # GPの更新

                mean, covariance = gp(data)

 

            if event.type == QUIT: # 終了が押された？

                return

            if (event.type == KEYDOWN and

                event.key  == K_ESCAPE): # ESCが押された？

                return

 

if __name__ == '__main__': main()