研究の掃溜ノオト
since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。
ガウス分布の逐次推定(平均と分散の更新式)
Key Words: ガウス分布 逐次推定 逐次学習 オンライン学習 パラメータ推定 平均値 分散
gaussian, normal distribution, sequential learning, online learning, parameter inference, mean, variance
データが従う確率密度関数(PDF)を推定することを考えましょう.
状況として
の2つが考えられますが今回は2の方に注目します.
gaussian, normal distribution, sequential learning, online learning, parameter inference, mean, variance
データが従う確率密度関数(PDF)を推定することを考えましょう.
状況として
- 予め全てのデータが与えられている
- データは時間をおいて逐次与えられる
の2つが考えられますが今回は2の方に注目します.
データがガウス分布に従っていると仮定するとPDFを同定するためにはデータの平均値と分散だけ求めればいいことになります. n個のデータが得られているとき平均値μnと分散σn2はそれぞれ
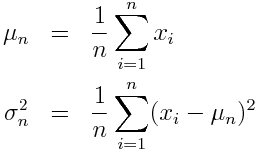
と定義されます.
さて今n+1個目の新しいデータが得られたとします. この時平均値と分散はどのようになるでしょうか. もちろん上式のnをn+1に変えて計算すれば求まります. しかし今までのデータをすべて保持しておくのはメモリ的に無駄が多いです. そこで前に計算した平均値μnと分散σn2と新しく得たデータxn+1だけから新たな平均値μn+1と分散σn+12を求めることを考えます. これが出来れば平均値と分散だけ保持していれば良いことになります.
結論から言うと平均値と分散の更新式は
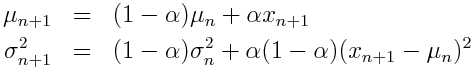
となります. ただし
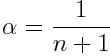
と置きました. もっともαに関しては予め定数で与えてしまうことが多いようです. こうすれば今までに得たデータの数を保持する必要もなくなります.
これでガウス分布の逐次学習ができましたね!データが来るたびに先述の更新式に従って平均値と分散を更新していけばいいだけです. 今回個人的にガウス分布の逐次学習方法を調べていて思ったのですが平均値の更新式は載っていても分散の更新式が載っていない資料がほとんどでした. ある資料には分散も平均値と同様に更新式が求まるとだけ書いてあったので自分で導出して見ることにしました. そして導出したのが先述の更新式です. それでは以下に平均値と分散の更新式の導出をそれぞれ載せて終わりたいと思います.
平均値の更新式の導出
平均値の定義より
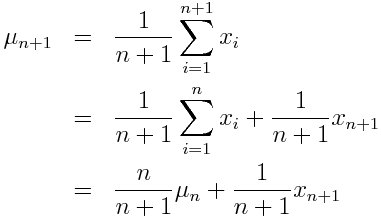
となり求まる.
分散の更新式の導出
これは少し骨が折れます.
今回の導出の方針は定義式から初めて
となります.
分散の定義より
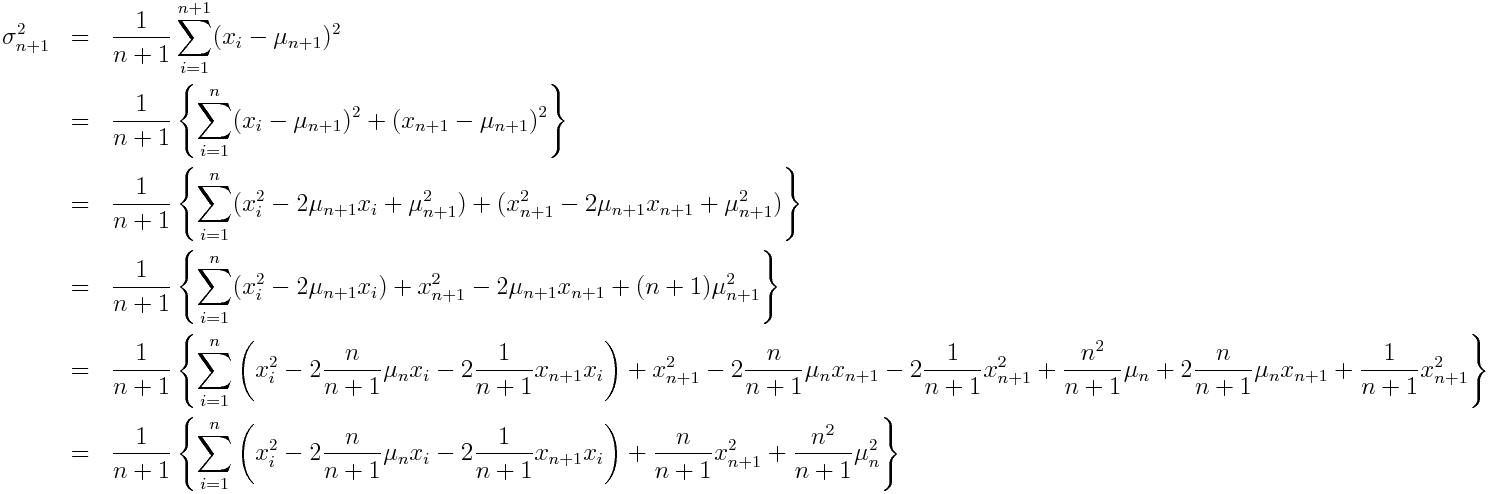
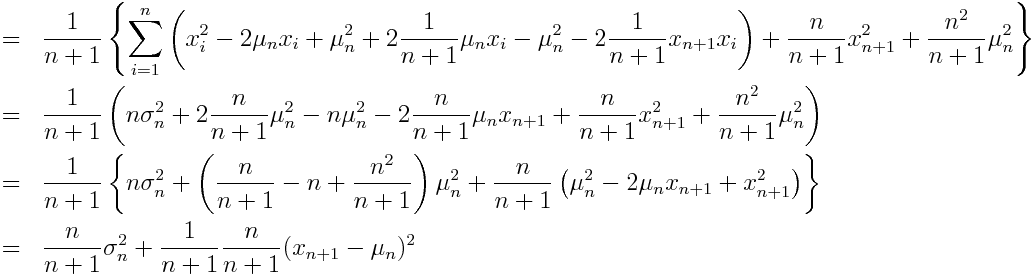
となり求まる.
と定義されます.
さて今n+1個目の新しいデータが得られたとします. この時平均値と分散はどのようになるでしょうか. もちろん上式のnをn+1に変えて計算すれば求まります. しかし今までのデータをすべて保持しておくのはメモリ的に無駄が多いです. そこで前に計算した平均値μnと分散σn2と新しく得たデータxn+1だけから新たな平均値μn+1と分散σn+12を求めることを考えます. これが出来れば平均値と分散だけ保持していれば良いことになります.
結論から言うと平均値と分散の更新式は
となります. ただし
と置きました. もっともαに関しては予め定数で与えてしまうことが多いようです. こうすれば今までに得たデータの数を保持する必要もなくなります.
これでガウス分布の逐次学習ができましたね!データが来るたびに先述の更新式に従って平均値と分散を更新していけばいいだけです. 今回個人的にガウス分布の逐次学習方法を調べていて思ったのですが平均値の更新式は載っていても分散の更新式が載っていない資料がほとんどでした. ある資料には分散も平均値と同様に更新式が求まるとだけ書いてあったので自分で導出して見ることにしました. そして導出したのが先述の更新式です. それでは以下に平均値と分散の更新式の導出をそれぞれ載せて終わりたいと思います.
平均値の更新式の導出
平均値の定義より
となり求まる.
分散の更新式の導出
これは少し骨が折れます.
今回の導出の方針は定義式から初めて
- ∑をxn+1について分ける
- 二乗を展開する
- μn+1についてある程度まとめる
- μn+1を展開する
- σn2をひっぱりだす
- ∑を適用する
- μnについて整理
- 全体を整理
となります.
分散の定義より
となり求まる.
PR
この記事へのトラックバック
トラックバックURL


この記事へのコメント