研究の掃溜ノオト

since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。

[PR]

[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。

Van der Pole Equation

振動現象は興味深い( ｰ`дｰ´)
その中でも興味深いのは Van der Pole 方程式によって記述される振動（以下VdP）です.

振動といえばバネですが, これは摩擦がなければ初めの振幅をずっと維持します.
しかしこのVdPはどんな初期値から始めても一定の軌道に収束します！
実際にVdP をシミュレーションしたのが以下の動画. 相空間上に格子状の初期値を持った粒子(?)を配置して時間発展を見たものです.

みんな一定の軌道になったでしょ？

Van der Pole 方程式を具体的に書き下すと以下のようになります.

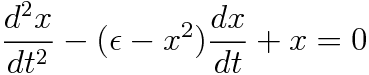
摩擦のあるバネの振動を記述する２階線形常微分方程式を扱ったことがある人なら分かると思いますが上式左辺の第２項は係数が正の時に摩擦の項を表しています. しかし第２項の係数が負になると摩擦とは逆に系全体にエネルギーを与えるような振る舞いをします. このバランスの結果として一つの安定した軌道に収束するのです.