研究の掃溜ノオト
since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。
圧縮センシングにおける観測行列の制限等長定数について
簡単に説明するともし得られるn次元データがスパース(値が0の成分が多い)なら
それを適当な線形変換(観測行列)でm次元に圧縮したものから逆にほとんど正確に推定することができるヨ!
って理論らしいです。つまり線形変換さえ知っていれば
データに対して持っている情報はm次元だけでいいというわけ。
例えば画像データなんかはDCT変換によって高周波成分はほとんど0になることが
知られていますからこの圧縮センシングを適用することができるわけです。
ボクも少し勉強したのですが数学的知識もそれほど必要なく
簡単に実装できそうだったので適当に画像でも圧縮しようかなー
とか考えていたら二つ壁が立ちふさがりました。ひとつは
線形計画法って何…(´・ω・`)
がんばれ理学部2回生。
えぇ知りませんでしたとも線形計画法。
正確には受験期に少しやった気はするのですが…
とりあえずこれは共立出版の「これなら分かる最適化数学」という本で勉強していますw
今シンプレックス法まで理解したのであと少し…
ふたつめは
観測行列って何を使えばいいの?(´・ω:;.:...
という問題です。いろいろ文献を呼んでいると皆さんランダム行列を使っているらしいので
実装するときはランダム行列を使えばいいのかなーと思ってはいるんですが、
ほんとにそんなやつに任せて大丈夫なんでしょうか!?
幸いこれには制限等長性という概念があって観測行列に関しては
その性能を評価できるようです!これは以下のようなもの
【制限等長定数】
与えられたm×n次元行列Aに対して任意のk-スパースなn次元ベクトルxを考えたとき
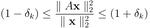
ここらへんは完全に最初にあげた文献そのままですw
違うのは制限等長定数を定義する式で行列のノルムを
類推させるような式に変形していることでしょうか!
このほうが数学勢には分かりやすい気がします。気がw
ここで初学者ながらに思いつくのは
なるほど与えられた行列の制限等長定数がわかればいいわけだな!
ってことです。
それで制限等長定数の求め方が書いてある文献を探してみたのですがそれが無く…
どうやらランダム行列の極限で制限等長定数の振る舞いを議論をするのが主流なようです。
しかし与えられたデータの次元は有限なので、どうしても観測行列の制限等長定数を
求めるアルゴリズムが知りたい・・・
なので自分で考えることにしました。
以下考えついたアルゴリズム。
制限等長定数の定義から
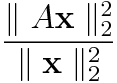
の大小を直接評価すればいいと思われる。
しかしこのままではxに定数倍の自由度があるので
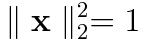
という条件を設ける。
ここでxの非0成分だけを順番に並べたベクトルをxk, 対応する列ベクトルだけ抜き出して並べたAの部分行列をAkとおきます。xkのノルムも1であることに注意してラグランジュの未定乗数法を用いるとラグランジュ関数は
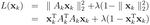
となることから結局Akに対してはその特異値の二乗の最大値と最小値で評価できることがわかりました。
後はこれを前組み合わせに対して適用してそのなかで最大最小値を取る特異値の二乗を用いれば元の式の
評価ができるというわけです(注1)。
求めた最大最小固有値をそれぞれλmax, λmin と置くとmax(λmax-1,1-λmin)が求める制限等長定数となります。
以上つらつらと考えた計算方法を述べたました。
問題点としては
・組み合わせの計算量が指数オーダー
・特異値の最小値が0になるかも…→つまり制限等長定数は常に1←最悪w(注2)
などが考えられます。
とにかく実装しないと始まらないですねー!w
近日中には早速画像圧縮をしてみたいと思います。
その時はまたブログに載せますね!
制限等長定数がもっと簡単に求まるとか
求め方の何処かに間違いがあるとか
求め方が載ってる論文があるよーとか
ございましたらどしどしコメントください!!><
待ってまーす。
画像がぼやけたあああああああああああああああああ(;゚Д゚)
注1
Akの特異値の二乗とはつまりAkTAkの固有値です!
注2
よく考えたら k<m であれば0になるとは限らず
これは当然の結果ですね!
数式書庫
(1-\delta_k) \leq \frac{\parallel A{\bf x}\parallel_2^2}{\parallel {\bf x}\parallel_2^2} \leq (1+\delta_k)
それを適当な線形変換(観測行列)でm次元に圧縮したものから逆にほとんど正確に推定することができるヨ!
って理論らしいです。つまり線形変換さえ知っていれば
データに対して持っている情報はm次元だけでいいというわけ。
例えば画像データなんかはDCT変換によって高周波成分はほとんど0になることが
知られていますからこの圧縮センシングを適用することができるわけです。
ボクも少し勉強したのですが数学的知識もそれほど必要なく
簡単に実装できそうだったので適当に画像でも圧縮しようかなー
とか考えていたら二つ壁が立ちふさがりました。ひとつは
線形計画法って何…(´・ω・`)
がんばれ理学部2回生。
えぇ知りませんでしたとも線形計画法。
正確には受験期に少しやった気はするのですが…
とりあえずこれは共立出版の「これなら分かる最適化数学」という本で勉強していますw
今シンプレックス法まで理解したのであと少し…
ふたつめは
観測行列って何を使えばいいの?(´・ω:;.:...
という問題です。いろいろ文献を呼んでいると皆さんランダム行列を使っているらしいので
実装するときはランダム行列を使えばいいのかなーと思ってはいるんですが、
ほんとにそんなやつに任せて大丈夫なんでしょうか!?
幸いこれには制限等長性という概念があって観測行列に関しては
その性能を評価できるようです!これは以下のようなもの
【制限等長定数】
与えられたm×n次元行列Aに対して任意のk-スパースなn次元ベクトルxを考えたとき
を満たすような最小の正の実数δkを制限等長定数と呼ぶ。
但しk-スパースなベクトルが非0な成分がk個以下のベクトルのことを指す。
【定理】
観測行列Aに対してδ2k < √2 - 1 が成り立つようなkが存在するとき任意のk-スパースなベクトルに対して正しい推定が行える。
但しk-スパースなベクトルが非0な成分がk個以下のベクトルのことを指す。
【定理】
観測行列Aに対してδ2k < √2 - 1 が成り立つようなkが存在するとき任意のk-スパースなベクトルに対して正しい推定が行える。
ここらへんは完全に最初にあげた文献そのままですw
違うのは制限等長定数を定義する式で行列のノルムを
類推させるような式に変形していることでしょうか!
このほうが数学勢には分かりやすい気がします。気がw
ここで初学者ながらに思いつくのは
なるほど与えられた行列の制限等長定数がわかればいいわけだな!
ってことです。
それで制限等長定数の求め方が書いてある文献を探してみたのですがそれが無く…
どうやらランダム行列の極限で制限等長定数の振る舞いを議論をするのが主流なようです。
しかし与えられたデータの次元は有限なので、どうしても観測行列の制限等長定数を
求めるアルゴリズムが知りたい・・・
なので自分で考えることにしました。
以下考えついたアルゴリズム。
制限等長定数の定義から
の大小を直接評価すればいいと思われる。
しかしこのままではxに定数倍の自由度があるので
という条件を設ける。
ここでxの非0成分だけを順番に並べたベクトルをxk, 対応する列ベクトルだけ抜き出して並べたAの部分行列をAkとおきます。xkのノルムも1であることに注意してラグランジュの未定乗数法を用いるとラグランジュ関数は
となることから結局Akに対してはその特異値の二乗の最大値と最小値で評価できることがわかりました。
後はこれを前組み合わせに対して適用してそのなかで最大最小値を取る特異値の二乗を用いれば元の式の
評価ができるというわけです(注1)。
求めた最大最小固有値をそれぞれλmax, λmin と置くとmax(λmax-1,1-λmin)が求める制限等長定数となります。
以上つらつらと考えた計算方法を述べたました。
問題点としては
・組み合わせの計算量が指数オーダー
・特異値の最小値が0になるかも…→つまり制限等長定数は常に1←最悪w(注2)
などが考えられます。
とにかく実装しないと始まらないですねー!w
近日中には早速画像圧縮をしてみたいと思います。
その時はまたブログに載せますね!
制限等長定数がもっと簡単に求まるとか
求め方の何処かに間違いがあるとか
求め方が載ってる論文があるよーとか
ございましたらどしどしコメントください!!><
待ってまーす。
画像がぼやけたあああああああああああああああああ(;゚Д゚)
注1
Akの特異値の二乗とはつまりAkTAkの固有値です!
注2
よく考えたら k<m であれば0になるとは限らず
これは当然の結果ですね!
数式書庫
(1-\delta_k) \leq \frac{\parallel A{\bf x}\parallel_2^2}{\parallel {\bf x}\parallel_2^2} \leq (1+\delta_k)
L({\bf x}_k)&=&\parallel A_k{\bf x}_k \parallel _2^2 + \lambda(1-\parallel {\bf x}_k \parallel _2^2)\\
&=&{\bf x}_k^{\rm T}A_k^{\rm T}A_k{\bf x}_k + \lambda(1-{\bf x}_k^{\rm T}{\bf x}_k)
\frac{1}{2}\frac{\partial L}{\partial {\bf x}_k}&=&A_k^{\rm T}A_k{\bf x}_k - \lambda{\bf x}_k = 0\\
A_k^{\rm T}A_k{\bf x}_k&=&\lambda{\bf x}_k\\
\parallel A_k{\bf x}_k\parallel_2^2&=&\lambda\parallel {\bf x}_k\parallel_2^2
PR
この記事へのトラックバック
トラックバックURL


この記事へのコメント