研究の掃溜ノオト
since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。
ガウス過程(Gaussian Process)による回帰分析プログラム
"Gaussian Process for Machine Learning"を読んでいたらどうしてもガウス過程がデータを観測するたびにうねうねと変化していく様子が見たくてつくりました!グラフ上をマウスでクリックしてそれを観測データとみなして回帰分析するプログラムです。カーネル特有のクリックするたびに(データが増えるたびに)計算時間が増えていくのを体感できます。特に開発環境が十進BASICなのでいっそう遅いですww
参考文献:www.gaussianprocess.org/gpml/chapters/RW.pdf
動作画像:
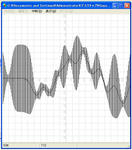
十進BASICソース
----------------------------------------------------------------------------------------------
参考文献:www.gaussianprocess.org/gpml/chapters/RW.pdf
動作画像:
十進BASICソース
----------------------------------------------------------------------------------------------
100 LET scaling = 1 !ガウスカーネルのスケーリングパラメーター
LET sigma = 0.05 !観測誤差
LET sca = 5 !分散の表示長さ調整用
!ガウスカーネル関数の定義
FUNCTION Kernel(x,y)
LET Kernel=EXP(-(x-y)^2/scaling^2)
END FUNCTION
!初期化
LET cnt = 0 !ループカウント
DIM dataset(1000,2) !クリック位置保存
DIM GRAM(1000,1000) !グラム行列のサイズ上限値
DIM IGRAM(1000,1000) !グラム行列の逆行列のサイズ上限値
DIM mean(200) !ガウス過程の平均値保存用
DIM var(200) !ガウス過程の分散保存用
!画面初期化
SET WINDOW -10,10,-10,10
DRAW GRID
!無情報事前分布表示
PLOT LINES:-10,0;10,0
FOR k = 1 TO 200
PLOT LINES:(k-100)/10,mean(k) + sca*(1+sigma);(k-100)/10,mean(k) - sca*(1+sigma)
NEXT k
PLOT LINES
!メインループ
DO
!マウスクリック待ち
DO
MOUSE POLL x,y,left,right
IF left = 0 THEN GOTO 200
LOOP
200 DO
MOUSE POLL x,y,left,right
IF left = 1 THEN GOTO 300
LOOP
!演算
300 LET cnt = cnt + 1
LET dataset(cnt,1) = x
LET dataset(cnt,2) = y
!行列のリサイズ
MAT GRAM = ZER(cnt,cnt)
MAT IGRAM = ZER(cnt,cnt)
!グラム行列の計算
FOR i = 1 TO cnt
FOR j = 1 TO cnt
LET GRAM(i,j) = Kernel(dataset(i,1),dataset(j,1))
NEXT j
LET GRAM(i,i) = GRAM(i,i) + sigma
NEXT i
MAT IGRAM = INV(GRAM)
!平均値と分散の計算
FOR k = 1 TO 200
LET var(k) = 1 + sigma
LET mean(k) = 0
FOR i = 1 TO cnt
FOR j = 1 TO cnt
LET var(k) = var(k) - (Kernel(dataset(i,1),(k-100)/10) * IGRAM(i,j) * Kernel(dataset(j,1),(k-100)/10))
LET mean(k) = mean(k) + (Kernel(dataset(i,1),(k-100)/10) * IGRAM(i,j) * dataset(j,2))
NEXT j
NEXT i
LET var(k) = sca * var(k)
NEXT k
!描画
CLEAR
DRAW GRID
!分散描画
FOR k = 1 TO 200
PLOT LINES:(k-100)/10,mean(k) + var(k);(k-100)/10,mean(k) - var(k)
NEXT k
PLOT LINES
!平均値描画
FOR k = 1 TO 200
PLOT LINES:(k-100)/10,mean(k);
NEXT k
PLOT LINES
!データ数表示
PRINT cnt
LOOP
END
PR
この記事へのトラックバック
トラックバックURL


この記事へのコメント