研究の掃溜ノオト
since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。
カテゴリー「未選択」の記事一覧
- 2025.04.27
[PR]
- 2011.07.07
Arduinoによるデバイス開発
- 2011.03.30
GPLVMで特徴抽出
- 2011.03.18
Gaussian Processes on Python
- 2011.02.19
こんなエラーが出ました
- 2011.02.17
ガウス過程(Gaussian Process)による回帰分析プログラム
Arduinoによるデバイス開発
今日、すごく久しぶりにマイコンを使う機会がありました。
しかも最近巷で流行っているArduino !
PICやH8、あとAVRをちょっと使ったことはあったのですが
Arduinoは手を出せていませんでした。まぁ載っているのはAVRですが。
実際に触ってみたらもう感動ですね。
使い方は
①箱から取り出してUSBでパソコンに繋ぐ。
②Arduinoのソフトをサイトから手に入れる(フリー)。
③プログラムする。
④コンパイル(Verify)して書きこむ(Upload)。
終わりですww
たったこれだけでマイコンプログラミングが出来るなんてwww
何がそんなに嬉しいのか?とお思いになるかもしれませんが、従来のマイコンなら
①まず書き込み回路を作る
②↑安定してうごかない
③↑配線が間違ってたから直す
④↑そもそも参考にしてたサイトの回路が動かないから別のサイトを当たる
それでやっと書き込み回路が完成したら
⑤A/Dの設定方法がわからない
⑥PWMの設定方法がわからない
⑦割り込みって何?
という始末www
こんなことは一切考えずにArduinoの開発は出来ちゃうんです!
マイコンの敷居もここまで低くなったか!って感じですね=w=
さて話を本題に戻しまして、Arduinoによるデバイスの開発についてですが
まずはロボットの作り方からお話しします。デバイスの作り方はおそらく←が分かれば何のことはないと思いますので。
ロボットを作るときに一番基本になるのは
①入力
②演算
③出力
この三つです。
入力とは外界の状態を”センサ”によって電気信号に変えてやったものですね。具体的に何を測ることができるのかは下に列挙しました。
演算はまさにArduinoが担当する部分ですね。入力は基本的に連続な電圧の変化(A/D)もしくは電源電圧かGNDか(1/0)になっていますがArduinoはどちらも読むことができます。その数値を元に演算(これは普通のC言語と同じようにできます)を行って出力の信号を出します。出力には1/0やPWMと呼ばれるものもあります。
出力は電気信号を元に外界に変化を与える物で具体的なものは以下に列挙しました。
□入力
光の強弱
・CdSセル
・フォトトランジスタ
音センサ(コンデンサマイク)
温度センサ
圧力センサ
測距センサ
加速度センサ
各加速度センサ(ジャイロ)
方位センサ
動体センサ
□出力
モーター
サーボモーター
ソレノイド
スピーカー
LED
これらのものを①②③と組み合わせてロボットを作ります。飽くまで基本ですが
例えば外の明るさによってLEDの明るさを変えるとか
人が来たことを検知してLEDをつけるとか
加速度センサ・各加速度センサとサーボモータを用いて自己位置を推定しながら動くロボットとか!
いろんなモノが作れます!
また、Arduinoであればセンサーの情報をパソコンに送ったり
パソコンからArduinoに命令を出してアクチュエータを動かすなどといったこともできるので
デバイス開発にも役に立つはずです!(通信にはシリアル通信を使うのかな?)
Musmeの開発もArduino の導入で一歩前進しそうです!
PR
GPLVMで特徴抽出
できてるかな??
もっと大きいファイルもあったのですが容量オーバーで上がらなかった・・・

もっと大きいファイルもあったのですが容量オーバーで上がらなかった・・・
Gaussian Processes on Python
Gaussian Processes のプログラムをPython+Pygame+Numpyの組み合わせで実装してみました。
クリックした点を通る関数をエラーバー付きで求めるというものです!
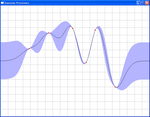
以下ソース
クリックした点を通る関数をエラーバー付きで求めるというものです!
以下ソース
# -*- coding: cp932 -*-
import pygame
from pygame.locals import *
from numpy import *
from numpy.linalg import *
from math import *
SCR_W = 800 # 表示ウィンドウの横幅
SCR_H = 600 # 表示ウィンドウの縦幅
GRIDCOLOR = 180 # グリッドのグレースケール
def Kernel(x,y): # 共分散関数
return exp(-((x-y)**2)/4000)
# return cos(0.5*(x-y))*exp(-((x-y)**2)/4000)
def gp(data): #各x軸での平均値と分散値の計算
mean = []
covariance = []
if len(data[0]) < 1 : # 事前分布
for x in range(800):
mean.append(0)
covariance.append(100.*Kernel(x,x))
return mean,covariance
num = len(data[0])
kfunc = zeros((num))
GRAM = zeros((num,num))
for i in range(num): # 共分散行列の計算
for j in range(num):
GRAM[i][j] = Kernel(data[0][i],data[0][j])
for i in range(num): # 観測ノイズの付加
GRAM[i][i] += 0.005
for x in range(800): # 各点の平均値と分散値の計算
for i in range(num):
kfunc[i] = Kernel(data[0][i],x)
mean.append(float(matrix(kfunc) * matrix(GRAM).I * matrix(data[1]).T))
covariance.append(float(100.*(Kernel(x,x) - matrix(kfunc) * matrix(GRAM).I * matrix(kfunc).T)))
return mean,covariance
def main():
data = [[],[]]
mean , covariance = gp(data) # 事前分布代入
origin = 300. * ones((800)) # 描画用原点の初期化
pygame.init() # pygameの初期化
screen = pygame.display.set_mode( (SCR_W, SCR_H) ) # 画面を作る
pygame.display.set_caption('Gaussian Processes') # タイトル
while 1:
pygame.draw.rect(screen , (255, 255, 255), (0, 0, 800, 600)) # 画面消去
for i in range(0,800,40): # グリッド描画
for j in range(0,600,40):
pygame.draw.line(screen, (GRIDCOLOR,GRIDCOLOR,GRIDCOLOR), (0,j), (800,j))
pygame.draw.line(screen, (GRIDCOLOR,GRIDCOLOR,GRIDCOLOR), (i,0), (i,600))
# 分散を多角形として描画
cov1 = zip(range(800),list(origin - array(mean)-array(covariance)))
cov2 = zip(range(800),list(origin - array(mean)+array(covariance)))
cov2.reverse()
pygame.draw.polygon(screen, (180,180,255), cov1+cov2, 0)
# 事後平均値関数の描画
pygame.draw.lines(screen, (0,0,0), False, zip(range(800),list(origin - array(mean))), 1)
if len(data[0])>0 : # プロット点の描画
for i in range(len(data[0])):
pygame.draw.circle(screen, (255,0,0), (int(data[0][i]), int(300. - data[1][i])), 3)
pygame.display.flip() # 画面を反映
for event in pygame.event.get(): # イベントチェック
if event.type == MOUSEBUTTONDOWN: # マウスボタン取得
# プロット点の代入
data[0].append(float(pygame.mouse.get_pos()[0]))
data[1].append(float(300. - pygame.mouse.get_pos()[1]))
# GPの更新
mean, covariance = gp(data)
if event.type == QUIT: # 終了が押された?
return
if (event.type == KEYDOWN and
event.key == K_ESCAPE): # ESCが押された?
return
if __name__ == '__main__': main()
こんなエラーが出ました
Uploadしたらこんな感じのエラーが出ました。
file.wreathlit.blog.shinobi.jp/994cc134.jpeg
file.wreathlit.blog.shinobi.jp/5244e196.jpeg
しましま
file.wreathlit.blog.shinobi.jp/994cc134.jpeg
file.wreathlit.blog.shinobi.jp/5244e196.jpeg
しましま
ガウス過程(Gaussian Process)による回帰分析プログラム
"Gaussian Process for Machine Learning"を読んでいたらどうしてもガウス過程がデータを観測するたびにうねうねと変化していく様子が見たくてつくりました!グラフ上をマウスでクリックしてそれを観測データとみなして回帰分析するプログラムです。カーネル特有のクリックするたびに(データが増えるたびに)計算時間が増えていくのを体感できます。特に開発環境が十進BASICなのでいっそう遅いですww
参考文献:www.gaussianprocess.org/gpml/chapters/RW.pdf
動作画像:
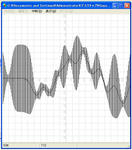
十進BASICソース
----------------------------------------------------------------------------------------------
参考文献:www.gaussianprocess.org/gpml/chapters/RW.pdf
動作画像:
十進BASICソース
----------------------------------------------------------------------------------------------
100 LET scaling = 1 !ガウスカーネルのスケーリングパラメーター
LET sigma = 0.05 !観測誤差
LET sca = 5 !分散の表示長さ調整用
!ガウスカーネル関数の定義
FUNCTION Kernel(x,y)
LET Kernel=EXP(-(x-y)^2/scaling^2)
END FUNCTION
!初期化
LET cnt = 0 !ループカウント
DIM dataset(1000,2) !クリック位置保存
DIM GRAM(1000,1000) !グラム行列のサイズ上限値
DIM IGRAM(1000,1000) !グラム行列の逆行列のサイズ上限値
DIM mean(200) !ガウス過程の平均値保存用
DIM var(200) !ガウス過程の分散保存用
!画面初期化
SET WINDOW -10,10,-10,10
DRAW GRID
!無情報事前分布表示
PLOT LINES:-10,0;10,0
FOR k = 1 TO 200
PLOT LINES:(k-100)/10,mean(k) + sca*(1+sigma);(k-100)/10,mean(k) - sca*(1+sigma)
NEXT k
PLOT LINES
!メインループ
DO
!マウスクリック待ち
DO
MOUSE POLL x,y,left,right
IF left = 0 THEN GOTO 200
LOOP
200 DO
MOUSE POLL x,y,left,right
IF left = 1 THEN GOTO 300
LOOP
!演算
300 LET cnt = cnt + 1
LET dataset(cnt,1) = x
LET dataset(cnt,2) = y
!行列のリサイズ
MAT GRAM = ZER(cnt,cnt)
MAT IGRAM = ZER(cnt,cnt)
!グラム行列の計算
FOR i = 1 TO cnt
FOR j = 1 TO cnt
LET GRAM(i,j) = Kernel(dataset(i,1),dataset(j,1))
NEXT j
LET GRAM(i,i) = GRAM(i,i) + sigma
NEXT i
MAT IGRAM = INV(GRAM)
!平均値と分散の計算
FOR k = 1 TO 200
LET var(k) = 1 + sigma
LET mean(k) = 0
FOR i = 1 TO cnt
FOR j = 1 TO cnt
LET var(k) = var(k) - (Kernel(dataset(i,1),(k-100)/10) * IGRAM(i,j) * Kernel(dataset(j,1),(k-100)/10))
LET mean(k) = mean(k) + (Kernel(dataset(i,1),(k-100)/10) * IGRAM(i,j) * dataset(j,2))
NEXT j
NEXT i
LET var(k) = sca * var(k)
NEXT k
!描画
CLEAR
DRAW GRID
!分散描画
FOR k = 1 TO 200
PLOT LINES:(k-100)/10,mean(k) + var(k);(k-100)/10,mean(k) - var(k)
NEXT k
PLOT LINES
!平均値描画
FOR k = 1 TO 200
PLOT LINES:(k-100)/10,mean(k);
NEXT k
PLOT LINES
!データ数表示
PRINT cnt
LOOP
END

