GPLVMで特徴抽出

 できてるかな？？
もっと大きいファイルもあったのですが容量オーバーで上がらなかった・・・

Gaussian Processes on Python

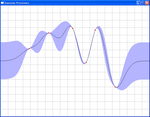
 Gaussian Processes のプログラムをPython+Pygame+Numpyの組み合わせで実装してみました。
クリックした点を通る関数をエラーバー付きで求めるというものです！



以下ソース

# -*- coding: cp932 -*-

import pygame

from pygame.locals import *

from numpy import *

from numpy.linalg import *

from math import *

 

SCR_W = 800 # 表示ウィンドウの横幅

SCR_H = 600 # 表示ウィンドウの縦幅

GRIDCOLOR = 180 # グリッドのグレースケール

 

def Kernel(x,y): # 共分散関数

    return exp(-((x-y)**2)/4000)

#    return cos(0.5*(x-y))*exp(-((x-y)**2)/4000)

 

def gp(data): #各ｘ軸での平均値と分散値の計算

    mean = []

    covariance = []

 

    if len(data[0]) < 1 : # 事前分布

        for x in range(800):

            mean.append(0)

            covariance.append(100.*Kernel(x,x))

        return mean,covariance

    

    num = len(data[0])

    kfunc = zeros((num))

    GRAM = zeros((num,num))

 

    for i in range(num): # 共分散行列の計算

        for j in range(num):

            GRAM[i][j] = Kernel(data[0][i],data[0][j])

    for i in range(num): # 観測ノイズの付加

        GRAM[i][i] += 0.005

 

    for x in range(800): # 各点の平均値と分散値の計算

        for i in range(num):

            kfunc[i] = Kernel(data[0][i],x)

        mean.append(float(matrix(kfunc) * matrix(GRAM).I * matrix(data[1]).T))

        covariance.append(float(100.*(Kernel(x,x) - matrix(kfunc) * matrix(GRAM).I * matrix(kfunc).T)))

    return mean,covariance

 

def main():

    data = [[],[]]

    mean , covariance = gp(data) # 事前分布代入

    origin = 300. * ones((800)) # 描画用原点の初期化

 

    pygame.init() # pygameの初期化

    screen = pygame.display.set_mode( (SCR_W, SCR_H) ) # 画面を作る

    pygame.display.set_caption('Gaussian Processes') # タイトル

 

    while 1:

        pygame.draw.rect(screen , (255, 255, 255), (0, 0, 800, 600)) # 画面消去

        for i in range(0,800,40): # グリッド描画

            for j in range(0,600,40):

                 pygame.draw.line(screen, (GRIDCOLOR,GRIDCOLOR,GRIDCOLOR), (0,j), (800,j))

                 pygame.draw.line(screen, (GRIDCOLOR,GRIDCOLOR,GRIDCOLOR), (i,0), (i,600))

 

        # 分散を多角形として描画

        cov1 = zip(range(800),list(origin - array(mean)-array(covariance)))

        cov2 = zip(range(800),list(origin - array(mean)+array(covariance)))

        cov2.reverse()

        pygame.draw.polygon(screen, (180,180,255), cov1+cov2, 0)

        # 事後平均値関数の描画

        pygame.draw.lines(screen, (0,0,0), False, zip(range(800),list(origin - array(mean))), 1)

        

        if len(data[0])>0 : # プロット点の描画

            for i in range(len(data[0])):

                pygame.draw.circle(screen, (255,0,0), (int(data[0][i]), int(300. - data[1][i])), 3)

 

        pygame.display.flip() # 画面を反映

 

        for event in pygame.event.get(): # イベントチェック

            if event.type == MOUSEBUTTONDOWN: # マウスボタン取得

                # プロット点の代入

                data[0].append(float(pygame.mouse.get_pos()[0]))

                data[1].append(float(300. - pygame.mouse.get_pos()[1]))

                # GPの更新

                mean, covariance = gp(data)

 

            if event.type == QUIT: # 終了が押された？

                return

            if (event.type == KEYDOWN and

                event.key  == K_ESCAPE): # ESCが押された？

                return

 

if __name__ == '__main__': main()

 

こんなエラーが出ました

Uploadしたらこんな感じのエラーが出ました。

file.wreathlit.blog.shinobi.jp/994cc134.jpeg
file.wreathlit.blog.shinobi.jp/5244e196.jpeg















しましま

ガウス過程(Gaussian Process)による回帰分析プログラム

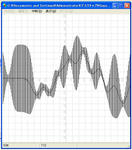
"Gaussian Process for Machine Learning"を読んでいたらどうしてもガウス過程がデータを観測するたびにうねうねと変化していく様子が見たくてつくりました！グラフ上をマウスでクリックしてそれを観測データとみなして回帰分析するプログラムです。カーネル特有のクリックするたびに（データが増えるたびに）計算時間が増えていくのを体感できます。特に開発環境が十進BASICなのでいっそう遅いですｗｗ

参考文献：www.gaussianprocess.org/gpml/chapters/RW.pdf

動作画像：



十進BASICソース
----------------------------------------------------------------------------------------------

100 LET scaling = 1     !ガウスカーネルのスケーリングパラメーター

    LET sigma = 0.05    !観測誤差

    LET sca = 5         !分散の表示長さ調整用

     

    !ガウスカーネル関数の定義

    FUNCTION Kernel(x,y)

       LET Kernel=EXP(-(x-y)^2/scaling^2)

    END FUNCTION

     

    !初期化

    LET cnt = 0               !ループカウント

    DIM dataset(1000,2)       !クリック位置保存

    DIM GRAM(1000,1000)       !グラム行列のサイズ上限値

    DIM IGRAM(1000,1000)      !グラム行列の逆行列のサイズ上限値

    DIM mean(200)             !ガウス過程の平均値保存用

    DIM var(200)              !ガウス過程の分散保存用

     

    !画面初期化 

    SET WINDOW -10,10,-10,10

    DRAW GRID

     

    !無情報事前分布表示

    PLOT LINES:-10,0;10,0        

    FOR k = 1 TO 200

       PLOT LINES:(k-100)/10,mean(k) + sca*(1+sigma);(k-100)/10,mean(k) - sca*(1+sigma)           

    NEXT k

    PLOT LINES

     

     

    !メインループ    

    DO

    !マウスクリック待ち

       DO

          MOUSE POLL x,y,left,right

          IF left = 0 THEN GOTO 200

       LOOP

200    DO

          MOUSE POLL x,y,left,right

          IF left = 1 THEN GOTO 300

       LOOP

        

       !演算

300    LET cnt = cnt + 1        

       LET dataset(cnt,1) = x

       LET dataset(cnt,2) = y

        

       !行列のリサイズ

       MAT GRAM = ZER(cnt,cnt)

       MAT IGRAM = ZER(cnt,cnt)

        

       !グラム行列の計算

       FOR i = 1 TO cnt

          FOR j = 1 TO cnt

             LET GRAM(i,j) = Kernel(dataset(i,1),dataset(j,1))

          NEXT j

          LET GRAM(i,i) = GRAM(i,i) + sigma

       NEXT i

       MAT IGRAM = INV(GRAM)

        

       !平均値と分散の計算       

       FOR k = 1 TO 200        

          LET var(k) = 1 + sigma

          LET mean(k) = 0

          FOR i = 1 TO cnt

             FOR j = 1 TO cnt

                LET var(k) = var(k) - (Kernel(dataset(i,1),(k-100)/10) * IGRAM(i,j) * Kernel(dataset(j,1),(k-100)/10))

                LET mean(k) = mean(k) + (Kernel(dataset(i,1),(k-100)/10) * IGRAM(i,j) * dataset(j,2)) 

             NEXT j

          NEXT i

          LET var(k) = sca * var(k)

       NEXT k

        

        

       !描画                

       CLEAR

       DRAW GRID      

        

       !分散描画        

       FOR k = 1 TO 200

          PLOT LINES:(k-100)/10,mean(k) + var(k);(k-100)/10,mean(k) - var(k)           

       NEXT k

       PLOT LINES

        

       !平均値描画

       FOR k = 1 TO 200

          PLOT LINES:(k-100)/10,mean(k);           

       NEXT k

       PLOT LINES

        

       !データ数表示

       PRINT cnt

        

    LOOP

     

 END

 

ランベルトのW関数

 指数関数と多項式が混ざった方程式を解くときによく出てくる”ランベルトのW関数”。
これは
f(x)=x*e^x
の逆関数として定義されています。
反復計算による関数値の計算法はよく知られているようです。
ちなみに
x=c*e^x
の解は
W(-c)
となります。
（両辺をexpで割って-1をかければ出るはず！）

参考文献：ランベルトのW関数(wikipedia)

W(c)を求める。10^1オーダーの計算で大体収束します。速いです！
Scilabソース
**********************************************************

//calculate W(z)

z=10;

//initial value

w1=0;

 

for i=1:20

    w2=w1-(w1*exp(w1)-z)/((exp(w1)*(w1+1)-(w1+2)*(w1*exp(w1)-z)/(2*w1+2)))

    w1=w2;

end

 

w1