研究の掃溜ノオト
since 2011/2/13 知能ロボ研究の合間に思ったこととか書いてます。
PCAの主成分を高速に求める方法について
主成分分析(PCA)はデータの圧縮手法の一つです.PCAを用いることでデータを拘束している高次元空間中の部分空間を取り出すことができます. 部分空間の基底を求める方法は一般には共分散行列の固有値問題に帰着されますが, 固有値問題は計算時間のオーダーがO(n^3)であるので次元が高いデータに対しては時間がかかりすぎてしまいます.しかしこれはすべての固有値・固有ベクトルを求める時の話であって, PCAに於いては値の大きい方から数個の固有値及び対応する固有ベクトルしか必要ないという場合が多々あるので真面目に固有値問題を解くのは効率がよくありません.
今回は数値計算の授業中に思いついたデータの主成分を効率よく必要な数だけ取ってくるアルゴリズムを紹介します. このアルゴリズムは大きい方から固有値及び対応する固有ベクトルを必要なだけ取ってくるアルゴリズムであるのでKPCAやCCA, KCCA などに応用することもできます. あとで調べて分かったのですがこの方法はGoogle がPagerank を求める時にも用いているそうです. 残念←
Principal Component Analysis (PCA) is one of the method of data compression. We can bring out the subspace in high dimension space which constrains data. Generally the method of calculate basis of the subspace is the eigenvalue problem of covariance matrix. However this method takes too long time for high dimension data because the eigenvalue problem takes time O(n^3). If you need not all eigenvalues and eigenvectors of covariance matrix and only need several these from the lager one, it is not efficient to solve the eigenvalue problem straight (in particular PCA).
In this item, I introduce the algorithm to calculate principal value of data efficiently as needed(I came up with this algorithm at the time of the lecture of numerical computation). This algorithm can be also applied to KPCA, CCA and KCCA because it calculate eigenvalues and eigenvectors of covariance matrix from the larger one as needed. Afterwards, I found this algorithm has already used by Google to calculate Pagerank.
今回は数値計算の授業中に思いついたデータの主成分を効率よく必要な数だけ取ってくるアルゴリズムを紹介します. このアルゴリズムは大きい方から固有値及び対応する固有ベクトルを必要なだけ取ってくるアルゴリズムであるのでKPCAやCCA, KCCA などに応用することもできます. あとで調べて分かったのですがこの方法はGoogle がPagerank を求める時にも用いているそうです. 残念←
Principal Component Analysis (PCA) is one of the method of data compression. We can bring out the subspace in high dimension space which constrains data. Generally the method of calculate basis of the subspace is the eigenvalue problem of covariance matrix. However this method takes too long time for high dimension data because the eigenvalue problem takes time O(n^3). If you need not all eigenvalues and eigenvectors of covariance matrix and only need several these from the lager one, it is not efficient to solve the eigenvalue problem straight (in particular PCA).
In this item, I introduce the algorithm to calculate principal value of data efficiently as needed(I came up with this algorithm at the time of the lecture of numerical computation). This algorithm can be also applied to KPCA, CCA and KCCA because it calculate eigenvalues and eigenvectors of covariance matrix from the larger one as needed. Afterwards, I found this algorithm has already used by Google to calculate Pagerank.
今回の中心となるアルゴリズムはべき乗法と呼ばれ行列の最大固有値を推定する手法として知られているものです[1,2].
Algorithm 1 - べき乗法(power method)
与えられたn次正方行列Aの最大固有値と対応する固有ベクトルを求める.
1. n次ベクトルx(0) を初期化する
2. x(n+1) = Ax(n) を計算する
3. x(n+1) を正規化する(||x(n+1)|| で割ってノルムを1にする)
4. 2-3をx(n) が収束するまで繰り返す
収束して得られたxが求める固有ベクトルである.
対応する固有ベクトルλは

と計算され行列Aの最大固有値となる.
このアルゴリズムは反復計算を含むが実際に計算してみると少ないステップで収束することが分かります.
これをデータの共分散行列に適用することで第一主成分を高速に求めることができます.
しかしこれでは第一主成分しか求めることができないので第二主成分以降を求めるには工夫が必要です.
ここで共分散行列が対称行列であることを思い出すと対称行列はスペクトル分解が可能である[3]ので固有値λと固有ベクトルvを用いて以下のように展開することができます.
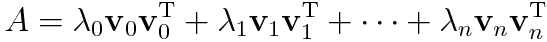
ただし, Aは共分散行列, nはデータの次元, λ0~λn は固有値で降順に並んでるとしv0~vn は対応する固有ベクトルとする.
今べき乗法によりλ0及びv0がわかっていたとすると, 上式をを変形して
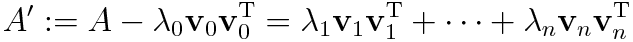
とすることにより元の行列において2番目に大きい固有値を最大固有値に持つ新たな行列A'を作ることができます.
そしてこの新たに得られた行列A'にべき乗法を適用することで元の行列における2番目に大きな固有値と固有ベクトルを求めることができるのです. 後は同様の作業を欲しい固有値の数だけ繰り返せば欲しい固有値と固有ベクトルを高速に求めることができます.
Algorithm 2 - べき乗法を用いて複数 固有値を求める方法
1. べき乗法を用いて行列の最大固有値λ及び固有ベクトルvを求める
2. 元の行列からλvvTを引く
3. 新たに得られた行列を用いてλが設定した値より低くなるか予め設定した回数が来るまで1~2を繰り返す.
これにより共分散行列の固有値を欲しい数だけ高速に求めることができるようになります.
具体的には固有値問題を解くアルゴリズムの計算オーダーが一般的にO(n^3)であったのに対し Algorithm2 の計算オーダーはO(n^2*i*m)(ただし i は反復回数, m は求める固有値の数)となるのでnが非常に大きな時は有効であることがわかります.
今回紹介したアルゴリズムは数値解析の基礎的な内容であり[2], Google のPagerank の計算にも用いられている手法である[4]のでぜひ一度試してみてはどうでしょうか.
参考文献
1. "第11章 行列の固有値・固有ベクトル計算" pdf
2. 森正武 「数値解析 第二版」共立出版
3. 行列のスペクトル分解 pdf
4. Google の秘密 - PageRank 徹底解説 web
Algorithm 1 - べき乗法(power method)
与えられたn次正方行列Aの最大固有値と対応する固有ベクトルを求める.
1. n次ベクトルx(0) を初期化する
2. x(n+1) = Ax(n) を計算する
3. x(n+1) を正規化する(||x(n+1)|| で割ってノルムを1にする)
4. 2-3をx(n) が収束するまで繰り返す
収束して得られたxが求める固有ベクトルである.
対応する固有ベクトルλは
と計算され行列Aの最大固有値となる.
このアルゴリズムは反復計算を含むが実際に計算してみると少ないステップで収束することが分かります.
これをデータの共分散行列に適用することで第一主成分を高速に求めることができます.
しかしこれでは第一主成分しか求めることができないので第二主成分以降を求めるには工夫が必要です.
ここで共分散行列が対称行列であることを思い出すと対称行列はスペクトル分解が可能である[3]ので固有値λと固有ベクトルvを用いて以下のように展開することができます.
ただし, Aは共分散行列, nはデータの次元, λ0~λn は固有値で降順に並んでるとしv0~vn は対応する固有ベクトルとする.
今べき乗法によりλ0及びv0がわかっていたとすると, 上式をを変形して
とすることにより元の行列において2番目に大きい固有値を最大固有値に持つ新たな行列A'を作ることができます.
そしてこの新たに得られた行列A'にべき乗法を適用することで元の行列における2番目に大きな固有値と固有ベクトルを求めることができるのです. 後は同様の作業を欲しい固有値の数だけ繰り返せば欲しい固有値と固有ベクトルを高速に求めることができます.
Algorithm 2 - べき乗法を用いて複数 固有値を求める方法
1. べき乗法を用いて行列の最大固有値λ及び固有ベクトルvを求める
2. 元の行列からλvvTを引く
3. 新たに得られた行列を用いてλが設定した値より低くなるか予め設定した回数が来るまで1~2を繰り返す.
これにより共分散行列の固有値を欲しい数だけ高速に求めることができるようになります.
具体的には固有値問題を解くアルゴリズムの計算オーダーが一般的にO(n^3)であったのに対し Algorithm2 の計算オーダーはO(n^2*i*m)(ただし i は反復回数, m は求める固有値の数)となるのでnが非常に大きな時は有効であることがわかります.
今回紹介したアルゴリズムは数値解析の基礎的な内容であり[2], Google のPagerank の計算にも用いられている手法である[4]のでぜひ一度試してみてはどうでしょうか.
参考文献
1. "第11章 行列の固有値・固有ベクトル計算" pdf
2. 森正武 「数値解析 第二版」共立出版
3. 行列のスペクトル分解 pdf
4. Google の秘密 - PageRank 徹底解説 web
PR
この記事へのトラックバック
トラックバックURL


この記事へのコメント